Draw Circle Matlab Passes Through 3 Point

To draw a straight line, the minimum number of points required is two. That means we tin can draw a straight line with the given two points. How many minimum points are sufficient to describe a unique circle? Is it possible to depict a circle passing through three points? In how many ways can we draw a circle that passes through 3 points? Well, permit's try to find answers to all these queries.

Learn: Circle Definition

Earlier drawing a circumvolve passing through 3 points, let's take a expect at the circles that take been fatigued through one and two points respectively.

Circumvolve Passing Through a Betoken

Let us consider a point and try to depict a circumvolve passing through that point.

As given in the figure, through a single indicate P, we can draw infinite circles passing through it.

Circle Passing Through 2 Points

Now, let united states accept ii points, P and Q and see what happens?

Once more we see that an infinite number of circles passing through points P and Q can exist fatigued.

Circle Passing Through Three Points (Collinear or Non-Collinear)

Allow us now accept 3 points. For a circle passing through 3 points, ii cases can arise.

• Three points can be collinear
• Three points can be non-collinear

Allow us study both cases individually.

Instance 1: A circumvolve passing through 3 points: Points are collinear

Consider three points, P, Q and R, which are collinear.

If iii points are collinear, whatever one of the points either prevarication outside the circle or inside it. Therefore, a circle passing through 3 points, where the points are collinear, is non possible.

Case 2: A circle passing through three points: Points are non-collinear

To draw a circle passing through three non-collinear points, we need to locate the middle of a circumvolve passing through 3 points and its radius. Follow the steps given below to understand how we can describe a circumvolve in this example.

Step 1: Have three points P, Q, R and join the points as shown below:

Pace 2: Draw perpendicular bisectors of PQ and RQ. Let the bisectors AB and CD meet at O such that the point O is chosen the centre of the circle.

Step 3: Depict a circle with O equally the middle and radius OP or OQ or OR. Nosotros get a circle passing through 3 points P, Q, and R.

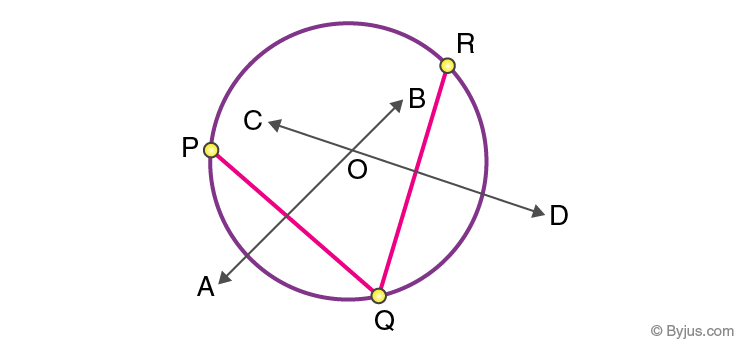
It is observed that but a unique circumvolve will pass through all three points. It can be stated as a theorem and the proof is explained equally follows.

It is observed that only a unique circumvolve volition pass through all three points. It can exist stated as a theorem, and the proof of this is explained below.

Given:

Three not-collinear points P, Q and R

To prove:

Only one circle tin can be fatigued through P, Q and R

Construction:

Join PQ and QR.

Depict the perpendicular bisectors of PQ and QR such that these perpendiculars intersect each other at O.

Proof:

S. No	Statement	Reason
i	OP = OQ	Every betoken on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment.
ii	OQ = OR	Every betoken on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment.
3	OP = OQ = OR	From (i) and (ii)
4	O is equidistant from P, Q and R

If a circle is drawn with O as middle and OP every bit radius, then it will also pass through Q and R.

O is the only bespeak which is equidistant from P, Q and R equally the perpendicular bisectors of PQ and QR intersect at O but.

Thus, O is the centre of the circle to be fatigued.

OP, OQ and OR will be radii of the circumvolve.

From higher up it follows that a unique circumvolve passing through 3 points tin be drawn given that the points are non-collinear.

Till at present, you lot learned how to draw a circle passing through iii not-collinear points. At present, yous will learn how to observe the equation of a circle passing through 3 points . For this we need to take three non-collinear points.

Circle Equation Passing Through 3 Points

Let's derive the equation of the circle passing through the 3 points formula.

Let P(10₁, y_one), Q(x₂, y₂) and R(x_three, y₃) be the coordinates of 3 non-collinear points.

We know that,

The general form of equation of a circle is: x² + y² + 2gx + 2fy + c = 0….(1)

Now, we need to substitute the given points P, Q and R in this equation and simplify to go the value of g, f and c.

Substituting P(10₁, y₁) in equ(one),

x₁ ⁱⁱ + y_one ² + 2gx_ane + 2fy₁ + c = 0….(2)

10₂ ² + y₂ ⁱⁱ + 2gx_ii + 2fy_ii + c = 0….(3)

10_three ² + y₃ ² + 2gx_three + 2fy₃ + c = 0….(iv)

From (ii) we get,

2gx_one = -x_one ^two – y₁ ² – 2fy₁ – c….(5)

Again from (2) nosotros get,

c = -x₁ ² – y₁ ⁱⁱ – 2gx₁ – 2fy₁….(half dozen)

From (4) we get,

2fy₃ = -x_three ² – y₃ ² – 2gx₃ – c….(7)

Now, subtracting (3) from (2),

2g(x₁ – x_ii) = (x_two ² -x_one ²) + (y₂ ² – y_i ⁱⁱ) + 2f (y₂ – y_ane)….(eight)

Substituting (6) in (7),

2fy3 = -x₃ ² – y₃ ⁱⁱ – 2gx₃ + x₁ ⁱⁱ + y_i ² + 2gx₁ + 2fy₁….(9)

Now, substituting equ(viii), i.eastward. 2g in equ(ix),

2f = [(x₁ ² – x_iii ²)(x₁ – 10_two) + (y_one ⁱⁱ – y₃ ² )(x₁ – x₂) + (x₂ ⁱⁱ – 10₁ ⁱⁱ)(10₁ – x₃) + (y₂ ² – y_ane ²)(x₁ – x₃)] / [(y_three – y_ane)(x₁ – x₂) – (y_two – y_one)(x₁ – ten_three)]

Similarly, we can go 2g equally:

2g = [(x_ane ² – ten₃ ²)(y₁ – 10₂) + (y₁ ^two – y_iii ^two)(y_i – y₂) + (x_two ² – x_ane ⁱⁱ)(y_ane – y_three) + (y₂ ² – y_i ²)(y_i – y₃)] / [(x₃ – ten₁)(y_i – y₂) – (10₂ – x_ane)(y₁ – y₃)]

Using these 2g and 2f values we can become the value of c.

Thus, by substituting g, f and c in (1) we will get the equation of the circle passing through the given three points.

Solved Example

Question:

What is the equation of the circle passing through the points A(2, 0), B(-2, 0) and C(0, 2)?

Solution:

Consider the general equation of circle:

10² + y² + 2gx + 2fy + c = 0….(i)

Substituting A(ii, 0) in (i),

(2)ⁱⁱ + (0)ⁱⁱ + 2g(ii) + 2f(0) + c = 0

4 + 4g + c = 0….(ii)

Substituting B(-ii, 0) in (i),

(-2)² + (0)² + 2g(-2) + 2f(0) + c = 0

4 – 4g + c = 0….(iii)

Substituting C(0, ii) in (i),

(0)² + (2)ⁱⁱ + 2g(0) + 2f(two) + c = 0

iv + 4f + c = 0….(four)

Calculation (ii) and (iii),

4 + 4g + c + 4 – 4g + c = 0

2c + 8 = 0

2c = -viii

c = -4

Substituting c = -iv in (ii),

4 + 4g – iv = 0

4g = 0

yard = 0

Substituting c = -4 in (iv),

4 + 4f – iv = 0

4f = 0

f = 0

Now, substituting the values of k, f and c in (i),

x² + y² + 2(0)x + 2(0)y + (-4) = 0

xⁱⁱ + y² – four = 0

Or

ten^two + y² = 4

This is the equation of the circle passing through the given iii points A, B and C.

To know more about the area of a circle, equation of a circle, and its properties download BYJU'Southward-The Learning App.

masseynowee1972.blogspot.com

Source: https://byjus.com/maths/circle-passing-through-3-points/

Share this post